تحليل الفرق بين مكعبين

                                             
                                                           الاهداف التعليمية

                                                  
١- تتعرف على الصورة العامة للفرق بين مكعبين .
 تشرح المعلمة الصورة العامة للفرق بين مكعبين .
الصورة العامة للفرق بين مكعبين هي :    س3–ص3

ما هي شروط الفرق بين مكعبين ؟؟

١- الحد الاول والحد الثاني كلاهما له جذر تكعيبي. 

2- الحدان بينهما اشارة فرق .












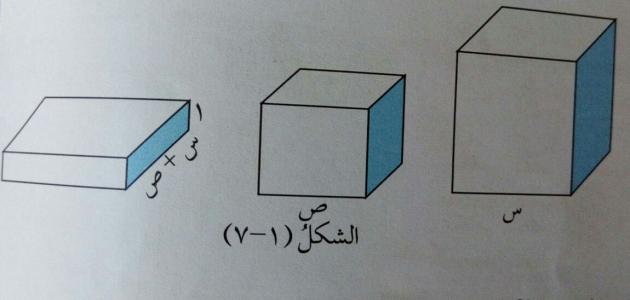
2- تحلل الفرق بين مكعبين الى عوامله الاولية .

تحليل الفرق بين مكعبين :  

س3–ص3= (س–ص) (س2+س ص+ص2)،
أمثلة على تحليل الفرق بين مكعبين

المثال الأول: حلل المقدار س3-125، الحل: حسب قانون الفرق بين مكعبين:

س3–ص3= (س–ص) (س2+س ص+ص2)، فإنّ: س3-125= (س-5) (س2+5س+25)

 المثال الثاني:  حلل المقدار (س+3)4-(س+3)، الحل: في البداية نقوم بإخراج (س+3) كعامل مشترك، لتصبح كالآتي:(س+3) 
((س+3)3-1) إذاً المقدار الأول = س+3، والمقداار الثاني = 1 (س+3) ((س+3)3-1)= (س+3) ((س+3)-1)((س+3)2+(س+3)+1))


تدريب 1 : حللي العبارات الى عواملها الاولية : 
1 -   ( ع-2 )3-ع3

2- 40 س3-5 ص3




3- تطبق الفرق بين مكعبين في اجراء العمليات الحسابية .
تدريب 2   :  حللي الى عواملها الاولية :  
1- س3-أ3

2- 64 س3ص3-64ع3








التقويم الختامي :  

حلّل المقدار 8 س3–27؟


https://www.youtube.com/watch?v=NTFyr8bHNBo